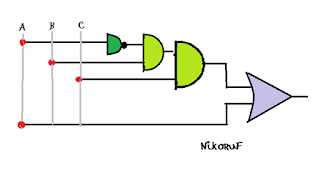
Anteriormente hablábamos de los túneles y que estos tendrían (o tienen) un sistema de ventiladores muy modernos. Increíblemente esto lo podemos controlar por medio de compuertas.
M (manipular manualmente el ventilador)= A
CO (alerta al dióxido de carbono excesivo)= B
Op (Despeja el humo que expulsan los camiones grandes)= C
A B C - Ventilador
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1
Ahora para formar la ecuación debemos sólo ver el A,B,C que lograron encender (1) el ventilador. Quedaría así:
Z=A'BC + AB'C' + AB'C + ABC' + ABC
A' (A negado) porque está en 0
B está en 1
C está en 1
Por lo tanto el ventilador está en 1
A=1
B (negado)=0
C(negado)=0
A=1
B(negado)=0
C=1
A=1
B=1
C(negado)= 0
A=1
B=1
C=1
Al hacer el plano con compuertas AND (pues estamos multiplicando) y al final OR (sumando) nos da un total de 18 compuertas. Es extenso para hacer en un circuito, pero hay una forma en la que podemos reducirlo por medio de los teoremas de Morgan (entrada anterior).
Haremos lo siguiente:
Z=A'BC + AB'C' + AB'C + ABC' + ABC
Lo subrayado en rojo tienen como común AB' por lo tanto dejaremos sólo uno y pondremos a C' + C en un paréntesis.
Z= A'BC + AB' (C'+ C)
Ahora
Z=A'BC + AB'C' + AB'C + ABC' + ABC
Aquí tenemos otra pareja en común, AB y de nuevo el complemento de C' y C.
Unificando quedaría así:
Z= A'BC + AB' (C'+ C) + AB (C'+ C)
Como en álgebra, estamos igualando valores para eliminar más rápido.
Luego seguimos reduciendo-
Z= A'BC + AB' + AB
(ya no aparece (C'+ C) porque como son el mismo con"signos" diferentes, es decir, uno positivo y otro negativo, se eliminan aunque aquí, queda 1 pero ya no aparecen en la operación)
y finalmente queda:
Z= A'BC + A
(B' y B se eliminaron)
Ahora se ha reducido de 18 compuertas a 3 compuertas.
Rincón Informáticamente informativo
martes, 16 de agosto de 2016
martes, 2 de agosto de 2016
Tunel Bogotá-Villavicencio
Para salir de Bogotá y entrar al hermoso llano necesitamos pasar unos muchos túneles los cuales si no me equivoco son 8 actualmente (luego serán 19), seis de estos vienen siendo cortos y otros dos largos, el de Boquerón y Buenavista.
Se iniciará la construcción del proyecto de doble calzada el cual tendrá un gran sistema de ventilación para que no mueras mientras respiras monóxido de carbono, esta ventilación tiene un sistema de detección de CO (Monoxido de Carbono), en caso de que no detecte monoxido de carbono la ventilación se desactivaría.
La iluminación es extensa, pero en las dos puntas hay un tipo de iluminación especial, que permite que no se dañen tus ojos por la iluminación dentro del túnel, aunque esto ya depende de la hora actual.
Hay postes SOS para caso de emergencia, por si ocurre un accidente o ese tipo de cosas.
En caso de un accidente, los operadores están atentos y vigilando desde cámaras, y se enviara una ayuda inmediata, ademas por medio de señalizaciones que estarán en todos lados,se informara sobre el estado de la vía y del accidente.
Actualmente, el riesgo (mas riesgoso) es el de adelantarse, si tu te adelantas tienes la posibilidad de chocarte con otro automóvil que este yendo a la dirección contraria.
 |
| Tomada de www.portafolio.co |
La iluminación es extensa, pero en las dos puntas hay un tipo de iluminación especial, que permite que no se dañen tus ojos por la iluminación dentro del túnel, aunque esto ya depende de la hora actual.
Hay postes SOS para caso de emergencia, por si ocurre un accidente o ese tipo de cosas.
En caso de un accidente, los operadores están atentos y vigilando desde cámaras, y se enviara una ayuda inmediata, ademas por medio de señalizaciones que estarán en todos lados,se informara sobre el estado de la vía y del accidente.
Actualmente, el riesgo (mas riesgoso) es el de adelantarse, si tu te adelantas tienes la posibilidad de chocarte con otro automóvil que este yendo a la dirección contraria.
martes, 26 de julio de 2016
TLM
Teoremas del álgebra de Boole
Anteriormente había una entrada en la que hablábamos de los operadores booleanos, pues en esta nueva actualización hablaremos de los teoremas de Boole. Por lo tanto veremos los operadores algebraicos (+), (-), (*) y un símbolo conocido para negar ( ' ) o recuerden la barra encima de las variables.
Recordemos:
(+) es el operador de la compuerta OR y (*) de AND.
Anteriormente había una entrada en la que hablábamos de los operadores booleanos, pues en esta nueva actualización hablaremos de los teoremas de Boole. Por lo tanto veremos los operadores algebraicos (+), (-), (*) y un símbolo conocido para negar ( ' ) o recuerden la barra encima de las variables.
Recordemos:
(+) es el operador de la compuerta OR y (*) de AND.
Teorema 1: Ley de identidad
AND OR
1*A= A 0+A=A
Teorema 2: Ley nula
AND OR
0*A=0 1+A=1
Teorema 3: Ley de idempotencia
AND OR
A*A=A A+A=A
Teorema 4: Ley de involución o inversa
AND OR
A*A'=0 A+A'=1
Teorema 5: Ley conmutativa
AND OR
A*B = B*A A+B = B+A
Teorema 6: Ley asociativa
AND OR
(A*B)*C = A*(B*C) (A+B)+C = A+(B+C)
Teorema 7: Ley distributiva
AND OR
A+B*C= (A+B)(A+C) A(B+C)= A*B + A*C
Teorema 8: Ley de absorción
AND OR
A(A+B)= A A+A*B= A
Leyes de Demorgan
Las primera ley de Morgan permite que convirtamos un producto que esté negado a una suma también...negada.
Veamos mejor:
AND
A'*B' = A'+B'
Mientras que la segunda hace todo lo contrario, una suma negada a un producto negado.
OR
A'+B' = A'*B'
Mapa de Karnaugh
Estos son la simplificación de los circuitos lógicos en el momento que tengamos una función lógica.
Escribiremos A' si A=0 o A si A=1. B' si B=0 o B si B=1 y C' si C=0 y C si C=1, así sucesivamente dependiendo de cuantas variables tengamos.
Contamos desde la segunda fila.
F= A'BC'+A'BC+AB'C'+AB'C+ABC'+ABC
martes, 19 de julio de 2016
Universalidad de la compuerta NAND
¡Chaaaann!
Las compuertas NAND son llamadas universales debido a que con ellas podremos formar las demás compuertas, es decir que podremos crear una compuerta OR combinando dos NAND. Veamos mejor un ejemplo:
Las compuertas NAND son llamadas universales debido a que con ellas podremos formar las demás compuertas, es decir que podremos crear una compuerta OR combinando dos NAND. Veamos mejor un ejemplo:
 |
| Compuerta OR formada con compuertas NAND |
Por lo tanto la tabla de valores que nos resultará, será la de OR. Tal cual.
A B X
0 0 0
0 1 1
1 0 1
1 1 1
- A0*B0= 0 como es un NAND entonces se niega y queda 1. B0*A0= 0 se niega y queda 1. tomamos los dos 1 que nos dieron de resultado y los multiplicamos entre sí en la salida. (Siempre multiplicaremos porque NAND tiene como operador la multiplicación). AB= 1*1= 1 pero es NAND entonces se niega y queda 0.
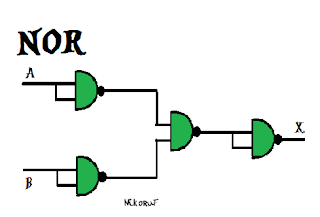
Compuerta NOR con compuertas NAND
Compuerta AND con compuertas NAND
Compuerta NOT con compuertas NAND
Compuerta XOR con compuertas NAND
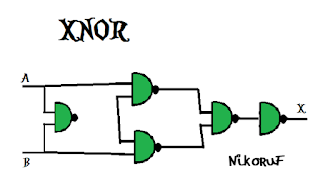
Compuerta XNOR con compuertas NAND
A continuación un ejemplo más para encontrar la tabla de verdad de las siguientes funciones.
X= (A*B) + (_A*B_) (_A*B_ la raya al piso representa la barra encima de las variables que significa que está negando).
1. Tenemos un AND, un NAND y un OR que pondremos como salida final. El OR representa el + en la función.
- A= 0 B=0
0*0= 0
Luego (_A*B_)
0*0=1
Ahora sumamos los resultados pues OR es la suma.
0+1= 1
1 es la salida.
- A=0 B=1
AND: 0*1= 0
NAND: 0*1=1
OR: 0+1= 1
- A=1 B=0
NAND: 1*0= 1
OR: 0+1= 1
- A=1 B=1
NAND: 1*1= 0
OR: 1+0= 1
Veremos en la tabla de la imagen que X es 1 en todas.
martes, 12 de julio de 2016
Compuertas Lógicas
Las compuertas lógicas son dispositivos electrónicos considerados como
la representación física, podría decirse, de los operadores matemáticos que
conocemos, (+, *), nos darán una función (en términos que no solemos entender,
se llaman funciones BOOLEANAS) que nos indicará si debemos sumar, multiplicar o
negar.
Así que ahora veremos las clases de compuertas lógicas que existen para
entender mejor esto.
Primeraaa.
Compuerta Separador (Yes) Seehh
Función booleana: X=A
Comenzando se debe aclarar que esta compuerta no tiene ningún operador
algebraico ya que solo tiene una entrada y una salida y su numero binario es el
mismo para ambas. Se usa para amplificar la señal.
A
X
0 0
Compuerta NOT (No)
X=_A (sólo imaginen que esa raya al piso está encima de la variable A, o
vean la imagen del final.)
Este invierte la señal, es decir niega los números binarios. Por eso se
llama NOT. Su símbolo es una barra encima de las variables A y B y cuantas
tengamos. Es decir, si A tuviera su binario en 1, le decimos NOT y esta
cambiará a 0, y viceversa.
A X
0 1
1 0
 |
| Símbolo de NOT |
Compuerta OR (ó)
X=A+B
Símbolo algebraico: (+) Suma.
Lo que debemos hacer cuando tengamos una compuerta OR es sumar. Esta
compuerta tiene dos entradas y una salida, pero puede tener mas entradas. La
tabla de verdades dice que si A o B o incluso ambas son 1, la salida será 1, si
no, será Zero.
A B X
0 0
0
0 1 1 >>>>> Encendido
1 0
1 >>>>> Encendido
1 1
1 >>>>> Encendido
 |
| Símbolo de OR |
Compuerta NOR
X=_A+B_
Como la compuerta NOT, es un complemento pero NOR niega los binarios de
OR, por eso hay un + es la "formula". Puede tener más de dos entradas
y una salida.
A B X
0 0
1
0
1 0
1 0
0
1 1
0
 |
| Símbolo de NOR |
Compuerta AND (o en spanish, Y)
X= A*B
Símbolo algebraico: (*) Multiplicación.
Esta compuerta tiene dos entradas que pertenecen a A y B llevandonos a
UNA salida, la salida X.
Para entender un poco más fácil es mejor ver la tabla de verdades que
usará los números binarios (Abajo la explicación de los números binarios) la
cual nos dice que si A y B están en el binario 1 la salida será 1 porque 1*1=1.
Es decir que las demás serán 0.
A B
X
0 0
0
0 1
0
1 0
0
1 1
1 >>>>> Encendido
Esta compuerta puede tener mas de dos entradas por lo que si queremos
que la salida sea 1 todas las entradas tienen que ser 1.
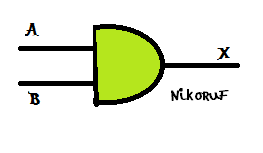 |
| Símbolo de AND |
Compuerta NAND (Not AND)
X=_A*B_
Esta es el complemento de AND, la cual negará los binarios de la
compuerta AND. Como AND, puede tener más de dos entradas.
A B X
0 0
1
0
1 0
1
0 0
1 1
0
 |
| Símbolo de NAND |
Compuerta XOR
X=A(+)B (En este caso, la función de XOR también tendrá el operador + pero
encerrado en un circulo. Como no sé cómo encerrarlo y no creo que se pueda lo
pondré en paréntesis.)
A B X
0 0
0
0 1
1
1
0 1
1 1
0 <<<<
En OR 1+1 nos daba 1, pero en este caso tendremos en cuenta la manera de
sumar binarios. Por eso sabemos que 1+1 es igual a 10 pero sólo tomaremos el
segundo digito que es 0, la salida será 0.
 |
| Símbolo de XOR |
Compuerta XNOR
X=_A(+)B_
¡Así es! Aquí negaremos XOR.
A B X
0 0
1
0 1
0
1
0 0
1 1
1
El circulo en el símbolo de NOT, NAND, NOR y XNOR expresa la negación.
martes, 5 de julio de 2016
Sistemas Numéricos
Números Decimales
Esta pequeña computadora y la que tú estás usando precisamente utiliza el sistema binario como una representación de los números para sus operaciones digitales. Por eso vamos a ver como convertir un número decimal a uno binario y viceversa.
1. Con cada uno de los dígitos comenzando de derecha a izquierda vamos a numerarlo con 20,21 22, 23, 24, 25,,......etc.
2. Procedemos a resolver cada potencia recordando que 20 es igual a 1 a menos que el dígito sea 0. Y finalmente sumamos los resultados para obtener el decimal.
3. Dicho anteriormente los dígitos 0 no se cuentan, sólo los 1.
Los números decimales son los que usamos diariamente como para decir nuestra edad, la fecha, contar, etc,etc. Lo que es fácil saber que se tratan de los diez primeros números (0,1,2,3,4,5,6,7,8 y 9) y continuaríamos tomando el 1 y el 0 para formar el...¡10! y así sucesivamente(11,...99,100...)
Números Binarios
 |
| Tomada de seminariomenorbenjamin.blogspot.com |
Por otro lado los números binarios sólo usa dos números, los cuales son el 0 y el 1. El cero al parecer no es tan inútil como pensamos.
.png) |
| Tomada de noticiascongabymia.blogspot.com |
Esta pequeña computadora y la que tú estás usando precisamente utiliza el sistema binario como una representación de los números para sus operaciones digitales. Por eso vamos a ver como convertir un número decimal a uno binario y viceversa.
Decimal a Binario
0
0
1
1
2
10
3
11
4
100
5
101
6
110
7
111
8
1000
9
1001
10
1010
Ahora comprobemos si 8 es igual a 1000.
1. Dividimos el número decimal entre 2.
2. Tomamos el último cociente que nos de más los residuos que serán siempre 0 y 1.
Binario a Decimal
Con el mismo ejemplo comprobemos si 1000 es igual a 8.
2. Procedemos a resolver cada potencia recordando que 20 es igual a 1 a menos que el dígito sea 0. Y finalmente sumamos los resultados para obtener el decimal.
3. Dicho anteriormente los dígitos 0 no se cuentan, sólo los 1.
Aquí otro ejemplo.
Suscribirse a:
Comentarios (Atom)