Compuertas Lógicas

Las compuertas lógicas son dispositivos electrónicos considerados como la representación física, podría decirse, de los operadores matemáticos que conocemos, (+, *), nos darán una función (en términos que no solemos entender, se llaman funciones BOOLEANAS) que nos indicará si debemos sumar, multiplicar o negar.

Así que ahora veremos las clases de compuertas lógicas que existen para entender mejor esto.

Primeraaa.

Compuerta Separador (Yes) Seehh

Función booleana: X=A

Comenzando se debe aclarar que esta compuerta no tiene ningún operador algebraico ya que solo tiene una entrada y una salida y su numero binario es el mismo para ambas. Se usa para amplificar la señal. 

              A    X

              0     0

              1     1  

Símbolo de YES

Compuerta NOT (No)

X=_A (sólo imaginen que esa raya al piso está encima de la variable A, o vean la imagen del final.)

Este invierte la señal, es decir niega los números binarios. Por eso se llama NOT. Su símbolo es una barra encima de las variables A y B y cuantas tengamos. Es decir, si A tuviera su binario en 1, le decimos NOT y esta cambiará a 0, y viceversa. 

            

            A   X

            0    1

            1    0   

Símbolo de NOT

Compuerta OR (ó)

X=A+B

Símbolo algebraico: (+) Suma.

Lo que debemos hacer cuando tengamos una compuerta OR es sumar. Esta compuerta tiene dos entradas y una salida, pero puede tener mas entradas. La tabla de verdades dice que si A o B o incluso ambas son 1, la salida será 1, si no, será Zero.

            

              A   B   X

              0    0    0

              0    1    1 >>>>> Encendido

              1    0    1 >>>>> Encendido

              1    1    1 >>>>> Encendido

Símbolo de OR

  

Compuerta NOR

X=_A+B_

Como la compuerta NOT, es un complemento pero NOR niega los binarios de OR, por eso hay un + es la "formula". Puede tener más de dos entradas y una salida. 

              A   B   X

              0    0    1

              0    1    0

              1    0    0

              1    1    0

Símbolo de NOR

Compuerta AND (o en spanish, Y)

X= A*B

Símbolo algebraico: (*) Multiplicación.

Esta compuerta tiene dos entradas que pertenecen a A y B llevandonos a UNA salida, la salida X.

Para entender un poco más fácil es mejor ver la tabla de verdades que usará los números binarios (Abajo la explicación de los números binarios) la cual nos dice que si A y B están en el binario 1 la salida será 1 porque 1*1=1. Es decir que las demás serán 0.

              A   B   X

              0    0    0

              0    1    0 

              1    0    0

              1    1    1 >>>>> Encendido

Esta compuerta puede tener mas de dos entradas por lo que si queremos que la salida sea 1 todas las entradas tienen que ser 1.

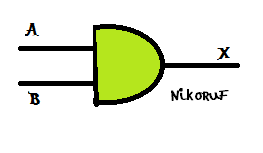Símbolo de AND

Compuerta NAND (Not AND)

X=_A*B_

Esta es el complemento de AND, la cual negará los binarios de la compuerta AND. Como AND, puede tener más de dos entradas.

              A   B   X

              0    0    1

              0    1    0

              1    0    0

              1    1    0

Símbolo de NAND

Compuerta XOR

X=A(+)B (En este caso, la función de XOR también tendrá el operador + pero encerrado en un circulo. Como no sé cómo encerrarlo y no creo que se pueda lo pondré en paréntesis.)

              A   B   X

              0    0    0                               

              0    1    1           

              1    0    1

              1    1    0 <<<<

En OR 1+1 nos daba 1, pero en este caso tendremos en cuenta la manera de sumar binarios. Por eso sabemos que 1+1 es igual a 10 pero sólo tomaremos el segundo digito que es 0, la salida será 0.

Símbolo de XOR

Compuerta XNOR

X=_A(+)B_

¡Así es! Aquí negaremos XOR.

              A   B   X

              0    0    1                               

              0    1    0           

              1    0    0

              1    1    1

Símbolo de XNOR

_______________________________

El circulo en el símbolo de NOT, NAND, NOR y XNOR expresa la negación.

 

Barra encima de las variables significa negación.