Universalidad de la compuerta NAND

¡Chaaaann!
Las compuertas NAND son llamadas universales debido a que con ellas podremos formar las demás compuertas, es decir que podremos crear una compuerta OR combinando dos NAND. Veamos mejor un ejemplo:
                                                                                           

Compuerta OR formada con compuertas NAND

Por lo tanto la tabla de valores que nos resultará, será la de OR. Tal cual.

A    B   X

0     0    0

0     1    1

1     0    1

1     1    1

• A0*B0= 0 como es un NAND entonces se niega y queda 1. B0*A0= 0  se niega y queda 1.   tomamos los dos 1 que nos dieron de resultado y los multiplicamos entre sí en la salida. (Siempre multiplicaremos porque NAND tiene como operador la multiplicación). AB= 1*1= 1 pero es NAND entonces se niega y queda 0.

Haremos esto con cada binario de la tabla de verdad para sacar la salida de la compuerta que queramos o tengamos que sacar. Claro, teniendo en cuenta la tabla de verdad de NAND.

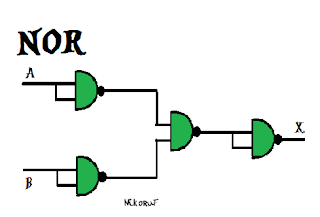
Compuerta NOR con compuertas NAND

Compuerta AND con compuertas NAND

Compuerta NOT con compuertas NAND

Compuerta XOR con compuertas NAND

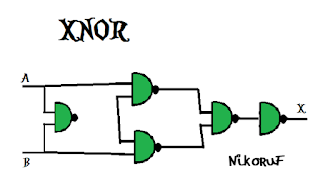
Compuerta XNOR con compuertas NAND

A continuación un ejemplo más para encontrar la tabla de verdad de las siguientes funciones.

X= (A*B) + (_A*B_) (_A*B_ la raya al piso representa la barra encima de las variables que significa que está negando).

1. Tenemos un AND, un NAND y un OR que pondremos como salida final. El OR representa el + en la función.

• A= 0   B=0

Primero (A*B)

0*0= 0

Luego (_A*B_)

0*0=1

Ahora sumamos los resultados pues OR es la suma.

0+1= 1

1 es la salida.

• A=0    B=1

Ahora con el siguiente.

AND: 0*1= 0

NAND: 0*1=1

OR: 0+1= 1

• A=1    B=0

AND: 1*0=0

NAND: 1*0= 1

OR: 0+1= 1

• A=1    B=1

AND: 1*1= 1

NAND: 1*1= 0

OR: 1+0= 1

Veremos en la tabla de la imagen que X es 1 en todas.